2x X 2 1 Derivative
DERIVATIVE OF ABSOLUTE VALUE FUNCTION
Let |f(10)| be an accented value part.
Then the formula to notice the derivative of |f(x)| is given below.
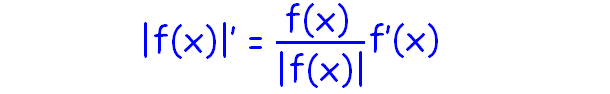
Based on the formula given, let us find the derivative of |x|.
|x|' = [x/|ten|](ten)'
|x|' = [10/|10|](ane)
|x|' = ten/|x|
Therefore, the derivative of |x| is x/|x|.
Let y = |ten|'.
Then, nosotros accept y = x/|x|.
In y = ten/|x|, if we substitute x = 0, the denominator becomes naught.
Since the denominator becomes null, y becomes undefined at 10 = 0
Permit us substitute some random values for ten in y.
when x = -3,
y = -three/|-3| = -3/3 = -1
when x = -2,
y = -2/|-2| = -2/2 = -1
when x = -1,
y = -1/|-one| = -1/1 = -1
when x = 0,
y = 0/|0| = 0/0 = undefined
when x = ane,
y = 1/|one| = 1/1 = 1
when 10 = 2,
y = 2/|2| = 2/2 = ane
when 10 = 3,
y = 3/|three| = iii/3 = one
Let u.s.a. summarize the to a higher place adding in table.
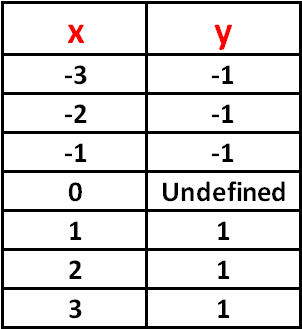
Now, based on the table given to a higher place, we can get the graph of derivative of |ten|.
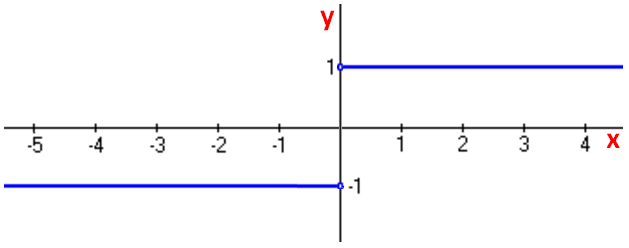
Discover the derivative of each of the following absolute value functions.
Example 1 :
|2x + 1|
Solution :
|2x + one|' = [( 2x + 1)/ |2x + one|] (2x + 1)'
= [(2x + one)/|2x + one|]( 2)
= 2( 2x + ane)/|2x + i|
Example ii :
|x3 + ane|
Solution :
| ten3 + ane|' = [( xthree + 1 )/ | ten3 + 1 |] ( x3 + 1 )'
= [( x3 + i )/| xiii + 1 |]( 3x ii)
= 3xtwo ( x3 + 1 )/| x3 + 1 |
Example iii :
|x|3
Solution :
In the given function | ten| iii , u sing chain dominion, first we have to notice derivative for the exponent 3 and and then for |x|.
(| x| 3)' = {3| x|2 } [ x /| x |] (x)'
= {3| 10|2 } [ 10 /| x |] (i)
= 3x| 10|
Instance four :
|2x - 5|
Solution :
|2x - v|' = [( 2x - 5)/ |2x - v|] (2x-five)'
= [(2x - 5)/|2x - 5|](2)
= two( 2x - 5)/|2x - 5|
Example 5 :
(10 - 2)2 + |ten - 2|
Solution :
{ (x - two) 2 + |x - 2|}' = [ (10 - two) 2 ]' + |x - 2|'
= 2 (x - 2) + [(x - ii)/|x - 2|]( x - two)'
= 2 (x - 2) + [(x - 2)/|10 - 2|] (one)
= 2 (ten - 2) + (10 - 2)/|ten - two|
Example 6 :
3|5x + 7|
Solution :
[3|5x+7|]' = 3 [(five x + 7)/ |5x + 7|] (5x+7)'
= 3 [(5 x + 7)/|5x + 7|]( 5)
= 15(5 10 + i)/|5x + 7|
Example 7 :
|sinx|
Solution :
|sinx|' = [sinx / |sinx|] (sinx)'
= [sinx/|sinx|] cosx
= (sinx ⋅ cosx)/|sinx|
Case viii :
|cosx|
Solution :
|cosx|' = [cosx / |cosx|] (cosx)'
= [cosx/|cosx|] (-sinx)
= -(sinx ⋅ cosx)/|cosx|
Example nine :
|tanx|
Solution :
|tanx|' = [tanx / |tanx|] (tanx)'
= [tanx/|tanx|] sec2 x
= (sec2 x ⋅ tanx)/|tanx|
Case 10 :
|sinx + cosx|
Solution :
|sinx + cosx|' = [(sinx + cosx) / |sinx + cosx|] (sinx + cosx)'
= [(cosx + sinx) / |sinx + cosx|] (cosx - sinx)
= (cos2 x - sinii x) / |sinx + cosx|
= cos2 x/|sinx + cosx|
Kindly postal service your feedback tov4formath@gmail.com
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
2x X 2 1 Derivative,
Source: https://www.onlinemath4all.com/derivative-of-absolute-value-function.html
Posted by: adamsexperearie.blogspot.com


0 Response to "2x X 2 1 Derivative"
Post a Comment